東大理系数学2015第2問(1)

$n$ 文字目と $n + 1$ 文字目の関係をみる

以下，$\mathrm{AA}$ を $\mathrm{A_1A_2}$ とおいて区別する。状態遷移図は下図のようになる。

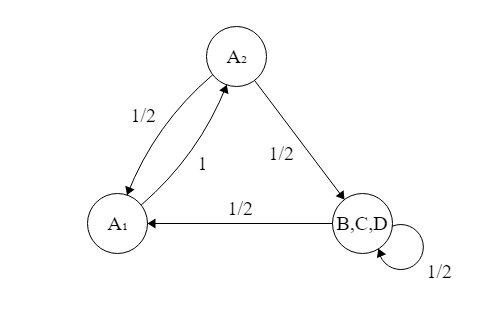
これと初期条件

• $1$ 文字目が $\mathrm{A_1}$ となる確率は $\frac{1}{2}$
• $1$ 文字目が $\mathrm{A_2}$ となる確率は $0$
• $1$ 文字目が $\mathrm{B, C, D}$ のいずれかとなる確率は $\frac{1}{2}$

より，本問は動的計画法で解くことができる。（求める確率は $n$ 文字目が $\mathrm{A_1}$ となる確率と $\mathrm{A_2}$ となる確率の和である。）

最初の $1$ 手で場合分けする

求める確率を $p_n$ とおく。

$1$ 回さいころを振ると，

• 確率 $\frac{1}{2}$ で $\mathrm{AA}$ が出たとき，残りの $n - 2$ 文字目が $\mathrm{A}$ となる確率は $p_{n - 2}$
• 確率 $\frac{1}{2}$ で $\mathrm{B, C, D}$ のいずれかが出たとき，残りの $n - 1$ 文字目が $\mathrm{A}$ となる確率は $p_{n - 1}$

となり，$p_n = \frac{1}{2} p_{n - 1} + \frac{1}{2} p_{n - 2}$ となる。

これと初期条件 $p_1 = \frac{1}{2}, p_2 = \frac{3}{4}$ より，本問は動的計画法で解くことができる。