問題 D2 とは制約と内容が異なります

問題文

$1$ から $N$ までの番号がついた $N$ 人の人がいて，さらに $1$ から $M$ までの番号がついた $M$ 個の友好関係があります．
友好関係 $i \scriptsize \hspace{0.3em} (1 \leq i \leq M)$ は人 $a_i$ と人 $b_i$ の間に友情があることを表し，「人 $a_i$ と人 $b_i$ とが互いに友達である」といいます．
ただし，自分同士と互いに友達であるような人は存在しません．

ここで「人 $s$ と人 $t$ とが友達の友達である」とは，$2$ 整数 $s, t \scriptsize \hspace{0.3em} (1 \leq s, t \leq N)$ が下記の条件を満たすことを指します．

• 下記の条件をすべて満たす整数 $v \scriptsize \hspace{0.3em} (1 \leq v \leq N)$ が存在する
  • 人 $s$ と人 $v$ とが互いに友達である
  • 人 $t$ と人 $v$ とが互いに友達である

下記の条件をすべて満たす正整数の組 $(p, q)$ は何通りあるか，求めてください．

• $1 \leq p < q \leq N$
• 人 $p$ と人 $q$ が友達の友達である

制約

• $1 \leq N \leq 3000$
• $0 \leq M \leq \mathrm{min}\, \{\, \frac{N(N-1)}{2},\, 3000\,\}$
• $1 \leq a_i < b_i \leq N \scriptsize \hspace{0.4em} (1 \leq i \leq M)$
• $i\neq j$ ならば $(a_i, b_i)\neq(a_j, b_j)$
• 入力はすべて整数である

入力

入力は以下の形式で標準入力から与えられる．

出力

答えを出力せよ．

サンプル

4 3
1 2
2 3
2 4

3

この友好関係を図に表すと次のようになります：

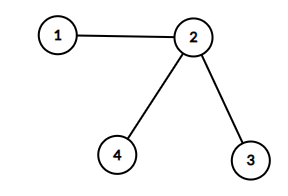
条件を満たす整数の組 $(p, q)$ は $(1, 3), (1, 4), (3, 4)$ の計 $3$ つです．

4 4
1 2
2 3
2 4
1 3

5

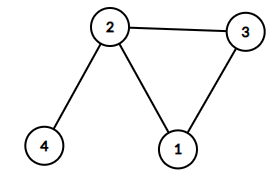
$(p, q) = (1, 2), (1, 3), (1, 4), (2, 3), (3, 4)$ のときに条件を満たします．
互いに友達であるような $2$ 人が，同時に友達の友達であるような関係もあり得ることに注意してください．

4 5
1 2
2 3
2 4
1 3
3 4

6

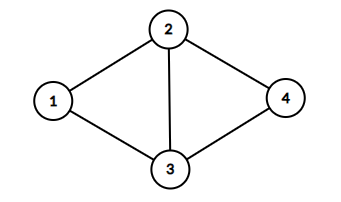
$(p, q) = (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)$ のときに条件を満たします．