解説
以下、 の場合を例に解説していきます。
- 黒い石の個数の求め方
オセロ盤の一辺は、 であり、単純に計算すると黒い石の個数は、 個となります。
しかし、オセロ盤の四隅で黒い石が重複しているため、黒い石の個数に気を付ける必要があります。
オセロ盤の四隅で重複している黒い石を除くと、黒い石の個数は 個となります。
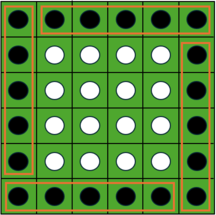
- 白い石の個数の求め方
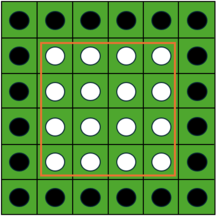
オセロ盤からオセロ盤の外周を除くと下の図のように一辺が の正方形になります。
したがって、白い石の個数は、 個となります。
後は、黒い石と白い石の個数を比べればよいです。