概要
数式とうまく対話して AC を手に入れましょう.
問題原案:kusirakusira
解説
Writer 解
正の整数 n,k を適当に固定します.
n-guesser において,k 回目の質問で Contestant 君が尋ねる実数は 2knr(r∈{1,3,…,2k−1}) と表されるものに限られることに着目します.
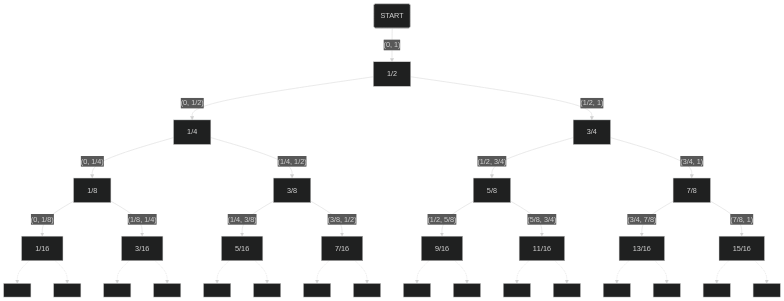
したがって,鍵 x がちょうど k 回目の質問によって特定されうるとき,x は以下の条件を満たします:
- x−2knr<21(r∈{1,3,…,2k−1})
これは必要条件ですが,十分条件ではないことに注意してください.k 回未満の質問によって特定されるような x の範囲も含まれています.
この問題で要求されていることは,(x,k)=(X,K) であるとき,ちょうど k 回目の質問で x が特定されるような整数 n の値を数え上げることです.
私たちの関心があるのは n なので,n について整理します:
- x−2knr<21x−21<2knr<x+21(2x−1)2k−1<nr<(2x+1)2k−1r1(2x−1)2k−1<n<r1(2x+1)2k−1⌊r1(2x−1)2k−1⌋<n<⌈r1(2x+1)2k−1⌉
- r∈{1,3,…,2k−1}
この条件を満たすような整数 n の集合を F(x,k) と書くことにすると,私たちの知りたい値は以下の集合の要素数です:
- F(X,K)∖1≤k<K⋃F(X,k)
これは,F(x,k) が 2k−1 個の区間の和集合であることに注目すると,たとえば imos 法を用いて worst Θ(K22K) 時間や expected Θ(K2K) 時間などで処理できます.
なお上述の議論では省略しましたが,n≥X という条件に注意してください.
解説:uni_kakurenbo
Tester 解
各質問において、 l と r のどちらが動いたかを考えてみます。
l=Ln,r=Rnとなるように実数 L,R を定めます。はじめ、 L=0,R=1 です。
Judge君が質問する実数は 21(l+r) です。ここで、 21(l+r)=Mn となるような実数 M を考えます。
l=Ln,r=Rn なので、21(l+r)=21(Ln+Rn)=2L+Rn となり、 M は L,R から計算することができます。
i (1≦i≦k−1) 回目の質問によって l と r のどちらが動いたかを考えます。
l が動いた場合、 Mn≦X−21⇔n≦MX−21 となり、 L=M となります。
r が動いた場合、 X+21≦Mn⇔MX+21≦n となり、 R=M となります。
これらの、 n の上限と下限を更新していくことで、 n としてあり得る区間を不等式で表すことができます。
この不等式を a≦n≦b ( a,b は実数)とします。
l,r が一回も動かない場合が存在しますが、 X≦n≦(X+21)2K なので、a の初期値を X 、 b の初期値を (X+21)2K などにしておけばよいです。
( n=(X+21)2K のとき、AAA君が i (1≦i≦K) 回目に質問する実数は (X+21)2K−i であり、これはどのようなiでも X+21 以上なので、 n はこれより小さいことがわかります)
k 回目の質問では l も r も動かずゲームが終了するので、 X−21<Mn<X+21⇔MX−21<n<MX+21 となります。
この不等式を c<n<d ( c,d は実数)とします。( c と d は必ず存在するので、実は a と b の初期値は明らかな上限と下限、例えば −1018 と 1018 などでもよいです)
a≦n≦b かつ c<n<d ( a,b,c,d は実数)であるような整数 n は O(1) で数え上げることができます。(参考:整数と実数と不等号と切り上げと切り捨て - noshi91のメモ)
結局、 l と r の動き方をすべて調べることで、条件を満たす整数nを数え上げることができます。また、それぞれの n-guesserに対しての l,r の動き方は一意に定まるため、数え上げた整数が重複することはありません。
よって、bit全探索や再帰関数などで l と r の動き方を 2K−1 通り全探索すれば、全体として Θ(K2K) や Θ(2K) で答えを求めることができます。
実装の補足(実数の変数について):
この問題では、 1≦X<240,1≦K≦12 なので、 0≦a,b,c,d<(X+21)2K<240×212=252 であり、仮数部が52bitであるC++のdoubleやPythonのfloat(デフォルトの浮動小数点数)などを用いて実装できます。また、 a,b,c,d はすべて有理数の四則演算で表すことができるので有理数であるため、分数で表し、分母と分子を持っておいて頑張って実装することも可能です。
解説:FplusFplusF
実装例
Writer 解
Tester 解
