概要
少し実装量が多めですが,一つ一つ課題を解決していくことで解くことができます.
また,少し深く考察をして実装量を減らすことも可能です.
問題原案:uni_kakurenbo
略解
先頭から求める
先頭 項を決定したとき,残りの 項は何通りの選び方ができるか とします.
をデクリメントして が 0-based の前提で考えると,求めるべき列の 項目は,先頭が であるような文字列のうち辞書順で 番目に小さいものであり,残りの 項は『 通りの選び方の中から辞書順で 番目に小さいもの』を求めればよいです.
結局,再帰的に同じ処理を繰り返して答えを求めることができます.(『カッコ内』がちょうど,大きさの小さい同様の問題になっています.)
は簡単な DP によって求めることができますが,その際は乗算のオーバーフローに注意してください.
末尾から求める
進法からの基数変換の要領で,末尾から順に求めていくこともできます.
先頭から求めていった場合に比べて,実装量は低減されるはずです.
解説
であるような の個数) とします.
先頭から順に決定する
先頭 項を決定したとき,残りの 項は何通りの選び方ができるか とします.
ですから,これは次に示すような DP によって の降順に 時間で計算できます.
以降 をデクリメントして が 0-based の前提で考えます.
求めるべき列の 項目は,先頭が であるような文字列のうち辞書順で 番目に小さいものであるといえます.
残りの 項は『 通りの選び方の中から辞書順で 番目に小さいもの』を求めればよいです.
この残った 項の求め方が,元の問題と全く同じということに気づいたでしょうか.
これを利用することで,次のように先頭から順々に求めていくことができます.
- 項目( 項のうちの先頭)を求める.
- これは 番目に小さいもの.
- 残りの 項目は, 通りの中で 番目に小さいもの.
- 項目(末尾 項のうちの先頭)を求める.
- これは 番目に小さいもの.
- 残りの 項目は, 通りの中で 番目に小さいもの.
- 項目(末尾 項のうちの先頭)を求める.
- 項目(末尾 項のうちの先頭)を求める.
- これは 番目に小さいもの.
- 残りは 項.
注記: のオーバーフロー対策
の制約を考えると, の値を求める段階でオーバーフローが生じてしまう可能性が非常に高いです.
これは, という制約を利用して,積が を超える場合は強制的に とするようにするとよいです.
( はデクリメントして 0-based で考えていることに注意してください.)
ABC169 - B でこれと同等の処理をする問題が出題されています.
末尾から順に決定する
より実装量の少ない解法を紹介します.
答えとなる列の 項目としてあり得る文字列が 通りあることは明らかです.
答えの 項目となる文字列を直接求めるのではなく,「答えの 項目は,それとしてあり得る 通りのもののうちで何番目に小さいものか」を求めるとします.
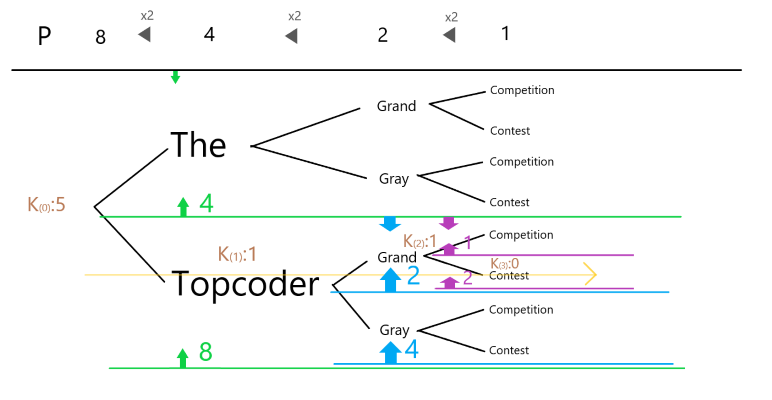
たとえば,入出力例 について考えてみます.
の値は簡単のために 0-based で考えたいので,デクリメントして とします.
- 項目としてあり得るものは,辞書順で昇順に
the,topcoderの 通り - 項目としてあり得るものは,辞書順で昇順に
grand,grayの 通り - 項目としてあり得るものは,辞書順で昇順に
competition,contestの 通り
です.
したがって,答えである,辞書順で 番目に小さい列 topcoder, grand, contest は,
- 項目は, 通りのうち 番目に小さい
topcoder - 項目は, 通りのうち 番目に小さい
grand - 項目は, 通りのうち 番目に小さい
contest
ですから, と表せることになります.(便宜上これらも 0-based で考えます.)
以降このような表記方法を「(文字列の列の)数列表現」と呼ぶこととします.
この数列を求めます.
この数列の各項について, 項目の数値は明らかに 以上 未満です.
もう一度入力例 に戻って考えます.
答えとしてあり得る列の数列表現を辞書順に列挙してみましょう.
これは,辞書順の定義より明らかに となります.
いかがですか?
以上 未満の数値を 進数で表記したものと全く同じであることがポイントです.
進数で与えられた は 進数に変換すると, ですから,先ほど考えた答えの列の数列表現とも一致します.
今回の入出力例 が,ちょうど 進数を用いて考えることができたのは, であったからです.
この考え方はより一般化することができ,あらゆる入力に対する答えの数列表現は「 桁目に, 以上 未満の 種類の数字を用いることができるような数値表現で, の値を表したときの各桁の値」に対応するといえます.
これは, 進表現から他の基数による表現へ変換する際と同じ要領で簡単に実装することが可能です.
時間計算量
いずれの解法でも,各 について先頭が であるような の(昇順に並び替えられた)一覧が必要です.
これは事前に一度 をソートすればよいので,全体を通しての時間計算量は となります.
発展
類題
- ABC 271 A - 484558
- ABC 169 B - Multiplication 2
- ABC 156 B - Digits
- ABC 234 C - Happy New Year!
- Typical90 067 - Base 8 to 9(★2)
- MojaCoder aab aba baa (Hard version) [Written by: @RedSpica]
実装例
C++
C++
Python
Python
余談
実装問題でごめんなさい...