概要
反射光の計算を頑張るのもよいですが,より簡単に・より高速に 解くことができます.
問題原案:uni_kakurenbo
解説
2 通りの解法を紹介します:
- タンジェントの加法定理を用いて反射の様子を実際にシミュレーションする.(やや重実装)
- 反射光を直線に展開して考える.(一行で書ける)
以下,直線 Px−Qy=0 を 鏡 S,直線 y=0 を 鏡 T と呼ぶことにします.
実際にシミュレーションをする解法
反射角を考える
θ,α,β をそれぞれ,鏡 S, 入射光, 反射光 の傾きとします.
反射の様子を考えると,これらの間に次のような関係が成り立つことが分かります:
- α+β=2θ

ここで,tanβ を tanθ(=QP) および tanα を用いて表すことを考えます.
tan の加法定理
- tan(θ0±θ1)=1∓tanθ0tanθ1tanθ0±tanθ1 (複号同順)
を用いると,
- tanβ=tan(2θ−α)=tanθ(2tanα−tanθ)+1tanθ(tanθtanα+2)−tanα
を得ます.
したがって,傾き k の光線が 鏡 S で反射した後の傾き k′ は次のように表されます:
- k′=t(2k−t)+1t(tk+2)−k
- ただし,t:=QP
なお,鏡 T で反射したときは,k′=−k です.
終了条件を考える
「以降反射が起こらない状態」(終了状態と呼ぶことにします) とはどのようなときか考えます.
それは以下をいずれも満たすときです:
- 光線が進む向きの x 成分が正
- 光線が 鏡 S に向かっているならば,光線の傾き k が t 以下
- 光線が 鏡 T に向かっているならば,光線の傾き k が 0 以上
後者 2 つは簡単に判定できますが,1 つ目は少々難しいです.
実は、反射光の傾きから進行方向の x 成分の符号を求めることができます.
- 光線が 鏡 S に向かっているとき:
- k<t のとき,負
- k=t のとき,平行 (終了状態に含まれる)
- k>t のとき,正
- 光線が 鏡 T に向かっているとき:
- k<0 のとき,正
- k=0 のとき,平行 (終了状態に含まれる)
- k>0 のとき,負
これらも,座標平面上での鏡と光線との様子を考えると分かります.
また,終了状態に初めて達したとき,「進行方向の x 成分の符号が入れ替わった」と判定されることも分かります.
最初の反射から終了状態までに,ちょうど 1 回だけ進行方向の x 成分の符号が反転するので,先ほどの式によって「進行方向の x 成分の符号が反転した」と 2 回目に判定されたとき,光線ははじめて終了状態に達しています.(前者 2 つの条件(傾きに関する条件)も満たされています.)
これをシミュレーションすればよいですが,上述の議論における各式の分母が 0 になる場合など,少々面倒な場合分けを行う必要があります.
詳細は実装例も参照してください.
なお,反射角を考える で得た α+β=2θ という関係を用いてシミュレーションを行うこともできます.
こちらの実装は軽めです.
反射光を直線に展開して考える解法
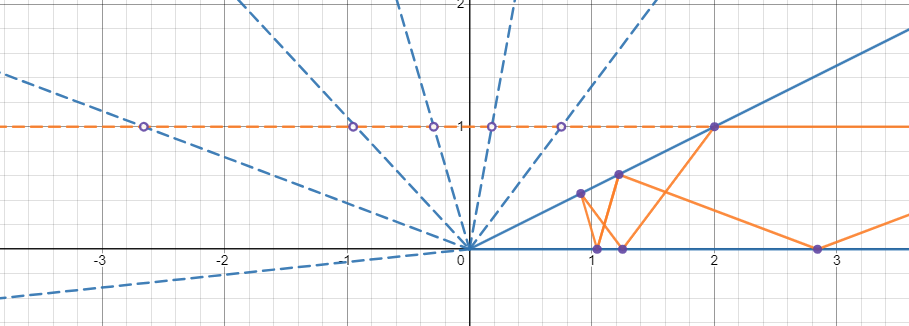
この図のように反射光は直進すると考えます.
θ=arctan(QP) とします.
図中の青色の点線の方程式は y=tan(kθ)(k=2,3,4,…) です.
すると,反射が起こる点と,図中の橙の線と青の線との交点 とが一対一に対応することが分かります.
したがって,直線 y=1 と y=tan(kθ)(k=1,2,3,…∧kθ<π) との交点の個数を数えればよいです.
また,これは kθ<π なる正の整数 k の個数に等しいですから,結局以下の値が答えに一致します:
- ⌈θπ⌉−1=⌈arctan(QP)π⌉−1
解説:uni_kakurenbo
実装例