Making a plan of breakfast

概要

DPと行列累乗を組み合わせて解くことができます。

DPテーブルの定義

以降では以下のDPテーブルについて考えます。

$dp[i][j] := i日目までの献立を決め、状態がjになる場合の数$

ただし、状態を以下のように定義します。

• 0:翌日以降の献立に制約なし
• 1:カレーパンを1日選択不可
• 2:小豆パンを1日選択不可
• 3:小豆パンを2日選択不可
• 4:カレーパンを1日、小豆パンを1日選択不可
• 5:カレーパンを1日、小豆パンを2日選択不可

DPテーブルの遷移

現状態と選んだパンによって、翌日の状態は以下の表のように決定されます。

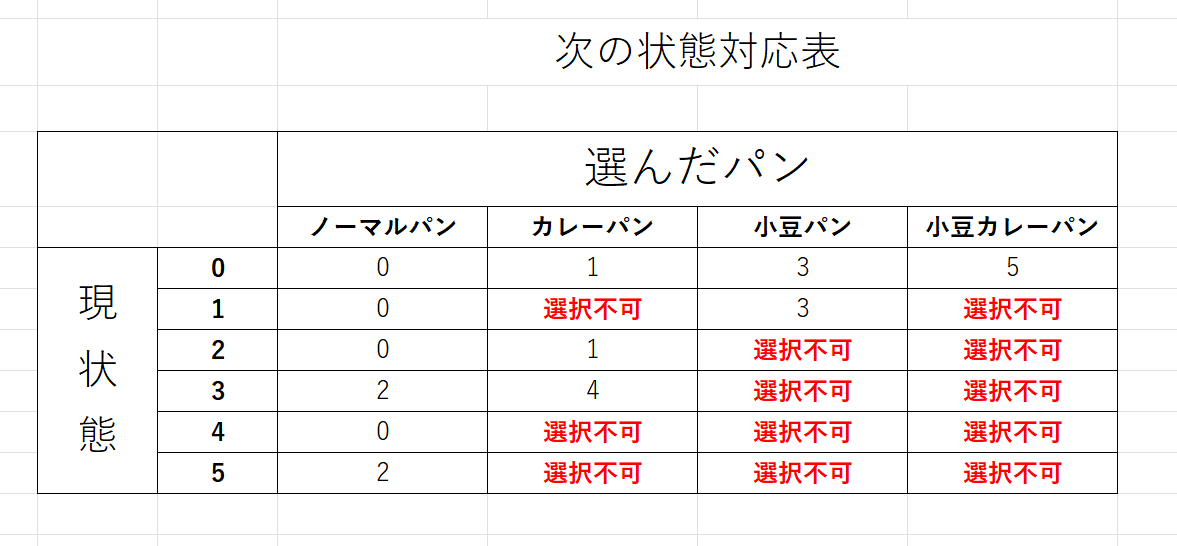
この表を漸化式で表すと、以下のようになります。

$$\left\{ \begin{array}{l} dp[i+1][0] &=& dp[i][0] + dp[i][1] + dp[i][2] + dp[i][4]\\ dp[i+1][1] &=& dp[i][0] + dp[i][2]\\ dp[i+1][2] &=& dp[i][3] + dp[i][5]\\ dp[i+1][3] &=& dp[i][0] + dp[i][1]\\ dp[i+1][4] &=& dp[i][3]\\ dp[i+1][5] &=& dp[i][0]\\ \end{array} \right.$$

さらに、これを行列の形で表すと、以下のようになります。

$$\begin{pmatrix} dp[i+1][0] \\ dp[i+1][1] \\ dp[i+1][2] \\ dp[i+1][3] \\ dp[i+1][4] \\ dp[i+1][5] \\ \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1 & 0 & 1 & 0\\ 1 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 1\\ 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ \end{pmatrix} \begin{pmatrix} dp[i][0] \\ dp[i][1] \\ dp[i][2] \\ dp[i][3] \\ dp[i][4] \\ dp[i][5] \\ \end{pmatrix}$$

初日に選ぶパンに制約がないことから、

$$\begin{pmatrix} dp[N][0] \\ dp[N][1] \\ dp[N][2] \\ dp[N][3] \\ dp[N][4] \\ dp[N][5] \\ \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1 & 0 & 1 & 0\\ 1 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 1\\ 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ \end{pmatrix} ^ N \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{pmatrix}$$

として、N日分の献立の場合の数を求めることができます。真ん中の遷移行列の$N$乗は繰り返し二乗法を用いた行列累乗のアルゴリズムによって、$O(\log N)$で求められます。