概要

$G$ の満たす性質をうまく利用しましょう．

問題原案：viral
改題：uni_kakurenbo

解説

任意の $2$ 非負整数 $u, v$ について $u \,\&\, v = u$ であることを $u \subseteq v$ と書きます． (bit の集合を想像してください．$u$ で立っているビットはすべて $v$ でも立っています．)

また，「$A[i] \subseteq A[j]$ のとき $i \to j$ の辺を張る」とありますが，記号の向きが逆で分かりづらいので「$A[i] \subseteq A[j]$ のとき $i \gets j$ の辺を張る」とします．このとき入次数が $0$ となる頂点の個数を数えます．

また，「任意の 3 非負整数 $u, v, w$ について『($u \subseteq v$ かつ $v \subseteq w$) ならば $u \subseteq w$』」であることは容易にわかります．(これを形式的に「推移律が満たされている」とも言います．)

また，「任意の相異なる 2 非負整数 $u, v$ について『$u \subseteq v$ ならば $u \subseteq v$ ではない』」ことも当然成り立ちます．(これを形式的に「反対称律が満たされている」ともいいます．)

以上のことを踏まえると，$A$ は distinct な (相異なる) ので，グラフ $G$ は 有向非循環 (DAG) になります．(これを形式的に「$\subseteq$ が非負整数全体の集合において半順序 (partial order) である」ともいいます．)

つまりトポロジカルソートしたときの末尾となる頂点の個数が分かればいいです．

---

問題文通りに辺を張ると $O(N^2)$ 本になって間に合いません．

なので「$\subseteq$ が非負整数全体の集合上で推移律を見たす」ことを利用して辺の本数を削減します．
具体的には，$A < 2^{20} < 2 \times 10^6$ の制約を利用します．

新たにグラフ $G'$ を考えます．$G'$ には頂点 $0, 1, 2, \ldots, 2^{20} - 1$ の $2^{20}$ 個の頂点があります． 各頂点について，「それぞれの頂点を表す非負整数から任意の 1 ビットを下げた頂点へ辺を張る」ことを行います．

$d = \mathrm{bit\_length}(A)$ とします．(この問題では $d \leq 20$)

より形式的には，頂点 $i$ からは，頂点 $i \,\&\, \tilde{2^0},\, i \,\&\, \tilde{2^1},\, i \,\&\, \tilde{2^2},\, \dots,\, i \,\&\, \tilde{2^d}$ (ただし自分以外) の $O(d)$ 個の頂点へ辺が張られます．

• 任意の非負整数 $u$ に対して $\tilde{u}$ は $u$ の bitwise NOT．

このようにすると，$\subseteq$ は推移律を満たすので，「任意の 2 非負整数 $u, v$ について『$u \subseteq v$ ならば $G'$ 上で $[u \gets v]$-path が存在する』」ということになります．

---

あとは $G'$ 上で DP を行えばよいです．($G'$ ももちろん DAG になります．)

• $\mathrm{DP}[x] \coloneqq (x \subsetneq A[i]$ を満たすような $1 \leq i \leq N$ なる整数 $i$ が存在する．$[\mathrm{True}/\mathrm{False}])$
• 初期状態：$\mathrm{DP}[x] = \mathrm{False} \scriptsize \; (0 \leq x \leq \max A)$
• 遷移：$\displaystyle \mathrm{DP}[y] = \bigvee_{G' \text{上で} [y \gets x]\text{-path} が存在する}(\mathrm{DP}[x] \lor (x ∈ A$ かどうか $[\mathrm{True}/\mathrm{False}]))$

詳しくは実装例も参照してください．

たとえば，$d = 3$ のときの $G'$ は次のようになります：

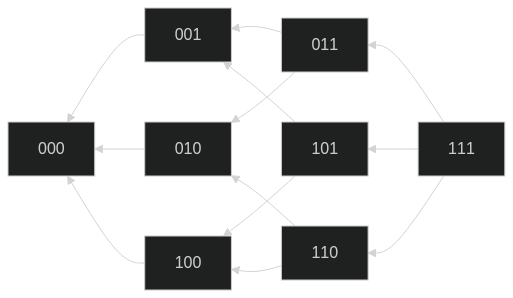
解説：uni_kakurenbo

実装例