G - Topological Heads

マルチテストについての説明はこちら (サンプル問題を確認されていない方のみお読みください。)

配点： 点

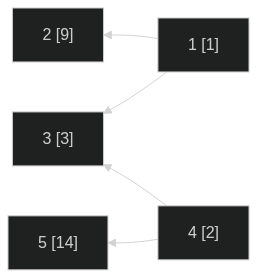
個の相異なる整数 と，各頂点に から までの番号が付けられた 頂点の有向グラフ があります．

ここで， なる任意の相異なる 整数 について であるとき，またそのときに限り， において 頂点 から 頂点 へ向かう有向辺が存在します．

• なお， 非負整数 に対して は の bitwise AND を表す．

の頂点であって出次数が であるものの個数を求めてください．

• 入力はすべて整数

各テストケースの入力は，それぞれ以下の形式で与えられる：

答えを出力せよ．

1
5
1 9 3 2 14

3

は次のようなグラフになります：

1
5
2 6 4 5 7

1

1
5
3 8 7 2 9

2