Statement
互いに区別できる1辺が長さの合同な正角形が無限にあります。
そのような正角形を以下の条件を満たすように個連結したとき、その図形には内外合わせて最大で何本の辺がありますか?
- 番目の正角形は番目と番目の正角形のみと連結されている
- 番目の正角形は存在するならば番目の正角形のみと、番目は存在するならば番目のみと連結されている
- 全ての正角形が他の正角形と重なり合わないように連結操作を行う
ただし、2つの正角形が連結であるとは以下のような状態であるとします
- 2 つの正角形が辺を 1 つ共有する
必要であれば、条件を満たす連結の仕方について入力例1や3を参考にしてください。
Constraints
Input
がスペースを空けて与えられる
Output
連結操作後の図形が持つ辺の数を答えよ。
Examples
Example1
input1
3 2
output1
5
3角形を条件を満たすように2つ連結するとその図形はちょうど5本の辺を持ちます。
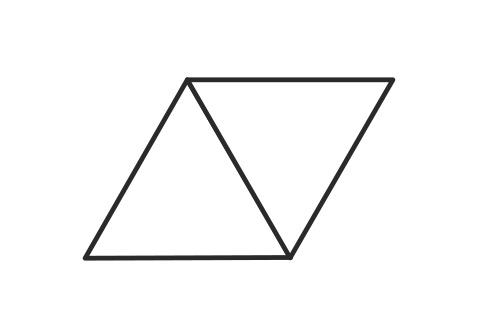
Example2
input2
4 1
output2
4
連結する必要はありません。
Example3
input3
6 3
output3
16
例えば以下のような連結の仕方が条件を満たします。
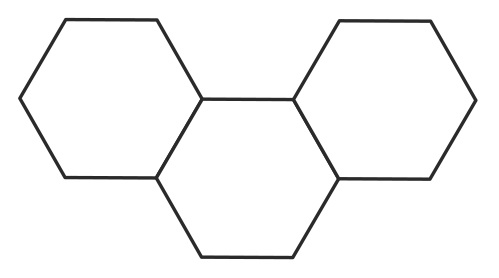
しかし、以下のような連結は条件を満たしていないことに注意してください。(どれを1, 3番目の正角形としても2つ目の条件を満たしていません)
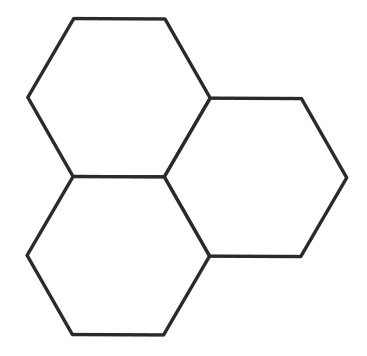
Submit
登録なしで提出できます。
Go (1.21)